It’s existential on the inside

This is the eighth of a series of articles on “Type Parameters and Type Members”. You may wish to check out the beginning, which introduces the PList type we refer to throughout this article without further ado.

When you start working with type parameters, nothing makes it immediately apparent that you are working with universal and existential types at the same time. It is literally a matter of perspective.

I will momentarily set aside a lengthy explanation of what this means, in favor of some diagrams.

Universal outside, existential inside

def fizzle[A]: PList[A] => PList[A] = {
  def rec(pl: PList[A], tl: PList[A]): PList[A] = tl match {
    case PNil() => pl
    case PCons(x, xs) => rec(PCons(x, pl), xs)
  }
  xs => rec(PNil(), xs)
}

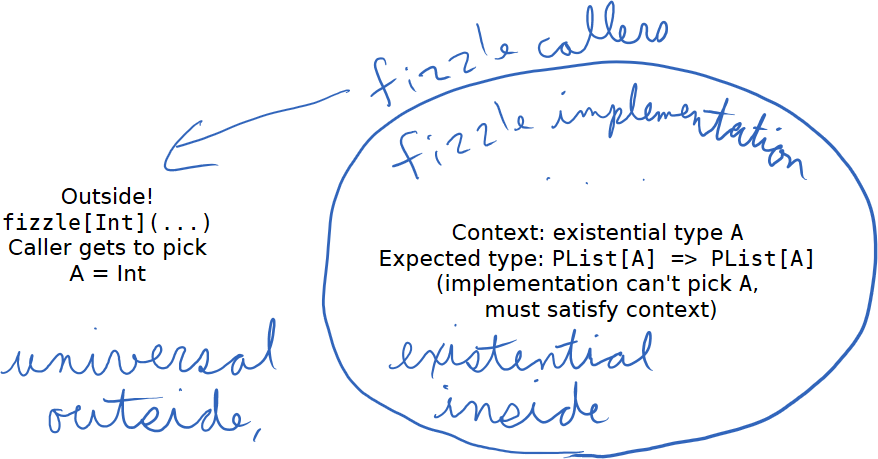
The caller can select any A, but the implementation must work with whatever A the caller chooses. So fizzle is universal in A from the outside, but existential in A from the inside.

So what happens when the caller and callee ‘trade places’?

Existential outside, universal inside

def wazzle: Int => PList[_] =
  n => if (n <= 0) PCons(42, PNil())
       else PCons("hi", PNil())

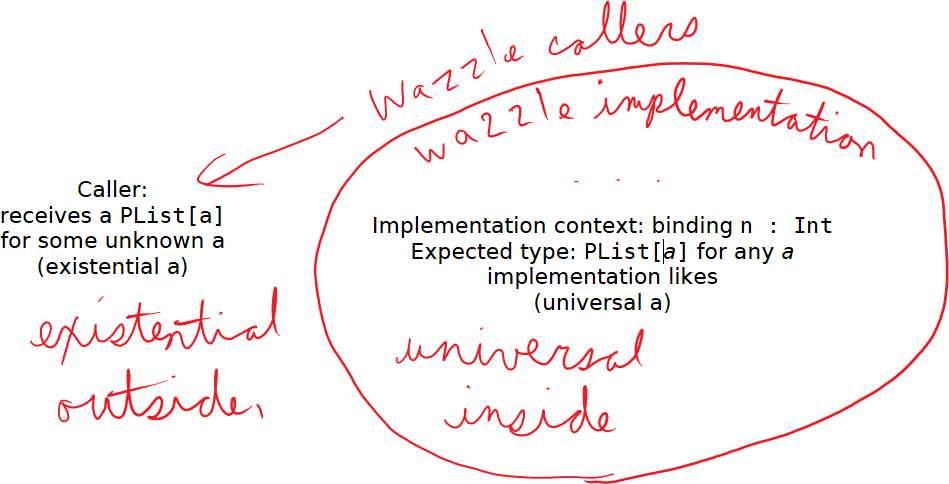
Now the implementation gets to choose an A, and the caller must work with whatever A the implementation chooses. So wazzle is universal in A from the inside, but existential in A from the outside.

A good way to think about these two, fizzle and wazzle, is that fizzle takes a type argument from the caller, but wazzle returns a type (alongside the list) to the caller.

Universal (!) outside, existential inside

def duzzle[A]: PList[A] => Int = {
  case PNil() => 0
  case PCons(_, xs) => 1 + duzzle(xs)
}

def duzzle2: PList[_] => Int = {
  case PNil() => 0
  case PCons(_, xs) => 1 + duzzle2(xs)
}

wazzle “returns” a type, alongside the list, because the existential appears as part of the return type. However, duzzle2 places the existential in argument position. So, as with all type-parameterized cases, duzzle among them, this is one where the caller determines the type.

We’ve discussed how you can prove that duzzle ≡_m duzzle2, in a previous post. Now, it’s time to see why.

Type parameters are parameters

The caller chooses the value of a type parameter. It also chooses the value of normal parameters. So, it makes sense to treat them the same.

Let’s try to look at fizzle’s type this way.

[A] => PList[A] => PList[A]

Existential types are pairs

If wazzle returns a type and a value, it makes sense to treat them as a returned pair.

Let’s look at wazzle’s type this way.

Int => ([A], PList[A])

This corresponds exactly to the forSome scope we have explored previously. So we can interpret PList[PList[_]] as follows.

PList[PList[A] forSome {type A}]  // explicitly scoped
PList[([A], PList[A])]            // “paired”

The duzzles are currying

With these two models, we can finally get to the bottom of duzzle ≡_m duzzle2. Here are their types, rewritten in the forms we’ve just seen.

[A] => List[A] => Int
([A], List[A]) => Int

Recognize that? They’re just the curried and uncurried forms of the same function type.

You can also see why the same type change will not work for wazzle.

Int => ([A], List[A])
[A] => Int => List[A]

We’ve moved part of the return type into an argument, which is…not the same.

The future of types?

This formulation of universal and existential types is due to dependently-typed systems, in which they are “dependent functions” and “dependent pairs”, respectively, though with significantly more expressive power than we’re working with here. They come by way of the description of the Quest programming language in “Typeful Programming” by Luca Cardelli, which shows in a clear, syntactic way that the dependent view of universal and existential types is perfectly cromulent to non-dependent type systems like Scala’s.

It is also the root of my frustration that Scala doesn’t support a forAll, like forSome but for universally-quantified types. After all, you can’t work with one without the other.

Now we have enough groundwork for “Making internal state functional”, the next part of this series. I suspect it will be a little prosaic at this point, though.